Computational geometry

点线多边形封装

const double pi = acos(-1.0);
const double eps = 1e-8;

// 判断 x 的大小，<0 返回 -1，>0 返回 1，==0 返回 0
int sgn(double x) { 
    if (fabs(x) < eps) return 0;
    else return x < 0 ? -1 : 1;
}

// 比较两个浮点数
int dcmp(double x, double y) { 
    if (fabs(x - y) < eps) return 0;
    else return x < y ? -1 : 1;
}

struct Point {
    double x, y;
    Point() {}
    Point(double x, double y) : x(x), y(y) {}

    Point operator + (const Point& B) const { return Point(x + B.x, y + B.y); }
    Point operator - (const Point& B) const { return Point(x - B.x, y - B.y); }
    Point operator * (double k) const { return Point(x * k, y * k); }
    Point operator / (double k) const { return Point(x / k, y / k); }

    bool operator == (const Point& B) const { 
        return sgn(x - B.x) == 0 && sgn(y - B.y) == 0; 
    }
    bool operator < (const Point& B) const {
        return sgn(x - B.x) < 0 || sgn(x - B.x) == 0 && sgn(y - B.y) < 0;
    }
};

typedef Point Vector;

class Geometry {
public:
    static double Distance(const Point& A, const Point& B) {
        return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y));
    }

    static double Dot(const Vector& A, const Vector& B) {
        return A.x * B.x + A.y * B.y;
    }

    static int AngleJudge(const Vector& A, const Vector& B) {
        return sgn(Dot(A, B));
    }

    static double Len(const Vector& A) {
        return sqrt(Dot(A, A));
    }

    static double Len2(const Vector& A) {
        return Dot(A, A);
    }

    static double Angle(const Vector& A, const Vector& B) {
        return acos(Dot(A, B) / Len(A) / Len(B));
    }

    static double Cross(const Vector& A, const Vector& B) {
        return A.x * B.y - A.y * B.x;
    }

    static double Area2(const Point& A, const Point& B, const Point& C) {
        return Cross(B - A, C - A);
    }

    static double AreaTriangle(const Point& A, const Point& B, const Point& C) {
        return Area2(A, B, C) / 2;
    }

    static Vector Rotate(const Vector& A, double rad) {
        return Vector(A.x * cos(rad) - A.y * sin(rad), A.x * sin(rad) + A.y * cos(rad));
    }

    static Vector Normal(const Vector& A) {
        double len = Len(A);
        return Vector(-A.y / len, A.x / len);
    }

    static bool Parallel(const Vector& A, const Vector& B) {
        return sgn(Cross(A, B)) == 0;
    }
};

class Line {
public:
    Point p1, p2;

    Line() {}
    Line(Point p1, Point p2) : p1(p1), p2(p2) {}
    Line(Point p, double angle) { 
        p1 = p;
        if (sgn(angle - pi / 2) == 0) { 
            p2 = p1 + Point(0, 1); 
        } else { 
            p2 = p1 + Point(1, tan(angle)); 
        }
    }
    Line(double a, double b, double c) { 
        if (sgn(a) == 0) {
            p1 = Point(0, -c / b);
            p2 = Point(1, -c / b);
        } else if (sgn(b) == 0) {
            p1 = Point(-c / a, 0);
            p2 = Point(-c / a, 1);
        } else {
            p1 = Point(0, -c / b);
            p2 = Point(1, (-c - a) / b);
        }
    }

    int PointLineRelation(const Point& p) const { 
        int c = sgn(Geometry::Cross(p2 - p1, p - p1));
        if (c < 0) return 1; // p 在 v 的右侧
        if (c > 0) return 2; // p 在 v 的左侧
        return 0; // p 在 v 上
    }

    bool PointOnSegment(const Point& p) const { 
        return sgn(Geometry::Cross(p - p1, p2 - p1)) == 0 &&
            sgn(Geometry::Dot(p - p1, p - p2)) <= 0;
    }

    double DistanceToPoint(const Point& p) const { 
        return fabs(Geometry::Cross(p - p1, p2 - p1)) / Geometry::Distance(p1, p2);
    }

    Point Projection(const Point& p) const { 
        double k = Geometry::Dot(p2 - p1, p - p1) / Geometry::Len2(p2 - p1);
        return p1 + (p2 - p1) * k;
    }

    Point SymmetryPoint(const Point& p) const { 
        Point q = Projection(p);
        return Point(2 * q.x - p.x, 2 * q.y - p.y);
    }

    static int LineRelation(const Line& v1, const Line& v2) { 
        if (sgn(Geometry::Cross(v1.p2 - v1.p1, v2.p2 - v2.p1)) == 0) {
            if (v1.PointLineRelation(v2.p1) == 0) return 1; // 重合
            else return 0; // 平行
        }
        return 2; // 相交
    }

    static Point CrossPoint(const Point& a, const Point& b, const Point& c, const Point& d) { 
        double s1 = Geometry::Cross(b - a, c - a);
        double s2 = Geometry::Cross(b - a, d - a);
        return Point(c.x * s2 - d.x * s1, c.y * s2 - d.y * s1) / (s2 - s1);
    }
};

typedef Line Segment;

class SegmentOps {
public:
    static bool CrossSegment(const Point& a, const Point& b, const Point& c, const Point& d) { 
        double c1 = Geometry::Cross(b - a, c - a);
        double c2 = Geometry::Cross(b - a, d - a);
        double d1 = Geometry::Cross(d - c, a - c);
        double d2 = Geometry::Cross(d - c, b - c);
        return sgn(c1) * sgn(c2) < 0 && sgn(d1) * sgn(d2) < 0;
    }

    static double DistanceToPoint(const Point& p, const Segment& v) { 
        if (sgn(Geometry::Dot(p - v.p1, v.p2 - v.p1)) < 0 || sgn(Geometry::Dot(p - v.p2, v.p1 - v.p2)) < 0)
            return std::min(Geometry::Distance(p, v.p1), Geometry::Distance(p, v.p2));
        return v.DistanceToPoint(p); // 点的投影在线段上
    }
};

class PolygonOps {
public:
    static int PointInPolygon(const Point& pt, const std::vector<Point>& p) { 
        int n = p.size();
        for (int i = 0; i < n; i++) {
            if (p[i] == pt) return 3; // 点在多边形顶点上
        }
        for (int i = 0; i < n; i++) {
            Line v = Line(p[i], p[(i + 1) % n]);
            if (v.PointOnSegment(pt)) return 2; // 点在边上
        }
        int num = 0;
        for (int i = 0; i < n; i++) {
            int j = (i + 1) % n;
            int c = sgn(Geometry::Cross(pt - p[j], p[i] - p[j]));
            int u = sgn(p[i].y - pt.y);
            int v = sgn(p[j].y - pt.y);
            if (c > 0 && u < 0 && v >= 0) num++;
            if (c < 0 && u >= 0 && v < 0) num--;
        }
        return num != 0; // 1：点在内部；0：点在外部
    }

    static double Area(const std::vector<Point>& p) { 
        double area = 0;
        int n = p.size();
        for (int i = 0; i < n; i++)
            area += Geometry::Cross(p[i], p[(i + 1) % n]);
        return area / 2; // 面积有正负
    }

    static Point Center(const std::vector<Point>& p) { 
        Point ans(0, 0);
        if (Area(p) == 0) return ans;
        int n = p.size();
        for (int i = 0; i < n; i++)
            ans = ans + (p[i] + p[(i + 1) % n]) * Geometry::Cross(p[i], p[(i + 1) % n]);
        return ans / Area(p) / 6;
    }
};

基础数值计算

const double pi = acos(-1.0);
const double eps = 1e-8;
int sgn(double x) { // 判断x的大小，<0返回-1，>0返回1，==0返回0
    if (fabs(x) < eps) return 0;
    else return x < 0 ? -1 : 1;
}
int dcmp(double x, double y) { // 比较两个浮点数
    if (fabs(x - y) < eps) return 0;
    else return x < y ? -1 : 1;
}

二维几何板子

点&向量

struct Point {
    double x, y;
    Point() {}
    Point(double x, double y) :x(x), y(y) {}
    Point operator + (Point B) { return Point(x + B.x, y + B.y); }
    Point operator - (Point B) { return Point(x - B.x, y - B.y); }
    Point operator * (double k) { return Point(x * k, y * k); }
    Point operator / (double k) { return Point(x / k, y / k); }
    bool operator == (Point B) { return sgn(x - B.x) == 0 && sgn(y - B.y) == 0; }
};
double Distance(Point A, Point B) {
    return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y));
}
typedef Point Vector; // 向量
double Dot(Vector A, Vector B) { return A.x * B.x + A.y + B.y; } // 点积
int angle_judge(Vector A, Vector B) {
    return sgn(Dot(A, B)); // 返回1表示A与B夹角为锐角，-1表示钝角，0表示直角
}
double Len(Vector A) { return sqrt(Dot(A, A)); } // 求向量A的长度
double Len2(Vector A) { return Dot(A, A); } // 求长度的平方，避免开方运算
double Angle(Vector A, Vector B) { return acos(Dot(A, B) / Len(A) / Len(B)); } // 求AB夹角
double Cross(Vector A, Vector B) { return A.x * B.y - A.y * B.x; } // 计算叉积A×B=|A||B|sinθ
double Area2(Point A, Point B, Point C) { return Cross(B - A, C - A); } // 计算两个向量构成的平行四边形的有向面积
double AreaTrangle(Point A, Point B, Point C) { return Area2(A, B, C) / 2; } // 三个点构成的三角形面积
Vector Rotate(Vector A, double rad) { // 将向量A逆时针旋转rad弧度
    // 逆时针旋转90°时 Rotate(A,pi/2)返回Vector(-A.y,A.x)
    // 顺时针旋转90°时 Rotate(A,-pi/2)返回Vector(A.y,-A.x)
    return Vector(A.x * cos(rad) - A.y * sin(rad), A.x * sin(rad) + A.y * cos(rad));
}
Vector Normal(Vector A) { return Vector(-A.y / Len(A), A.x / Len(A)); } // 求单位法向量
bool Parallel(Vector A, Vector B) { return sgn(Cross(A, B)) == 0; } // 返回true表示平行或重合
struct Line {
    Point p1, p2;
    Line() {}
    Line(Point p1, Point p2) :p1(p1), p2(p2) {}
    Line(Point p, double angle) { // 点和角度确定直线
        p1 = p;
        if (sgn(angle - pi / 2) == 0) { p2 = (p1 + Point(0, 1)); }
        else { p2 = (p1 + Point(1, tan(angle))); }
    }
    Line(double a, double b, double c) { // ax + by + c = 0
        if (sgn(a) == 0) {
            p1 = Point(0, -c / b);
            p2 = Point(1, -c / b);
        }
        else if (sgn(b) == 0) {
            p1 = Point(-c / a, 0);
            p2 = Point(-c / a, 1);
        }
        else {
            p1 = Point(0, -c / b);
            p2 = Point(1, (-c - a) / b);
        }
    }
};

直线&线段

typedef Line Segment; // 线段
int Point_line_relation(Point p, Line v) { // 判断点和直线的位置关系
    int c = sgn(Cross(p - v.p1, v.p2 - v.p1));
    if (c < 0) return 1; // p在v的右侧
    if (c > 0) return 2; // p在v的左侧
    return 0; // p在v上
}
bool Point_on_seg(Point p, Line v) { // 判断点p是否在线段v上
    // 原理：共线的前提下判断p和v的两个端点产生的角是否为钝角（180°）
    return sgn(Cross(p - v.p1, v.p2 - v.p1)) == 0 &&
        sgn(Dot(p - v.p1, p - v.p2)) <= 0;
}
double Dis_point_line(Point p, Line v) { // 点到直线距离
    return fabs(Cross(p - v.p1, v.p2 - v.p1)) / Distance(v.p1, v.p2);
}
Point Point_line_proj(Point p, Line v) { // 点在直线上的投影
    double k = Dot(v.p2 - v.p1, p - v.p1) / Len2(v.p2 - v.p1);
    return v.p1 + (v.p2 - v.p1) * k;
}
Point Point_line_symmetry(Point p, Line v) { // 点关于直线的对称点
    Point q = Point_line_proj(p, v);
    return Point(2 * q.x - p.x, 2 * q.y - p.y);
}
double Dis_point_seg(Point p, Segment v) { // 点到线段的距离
    if (sgn(Dot(p - v.p1, v.p2 - v.p1)) < 0 || sgn(Dot(p - v.p2, v.p1 - v.p2)) < 0)
        return min(Distance(p, v.p1), Distance(p, v.p2));
    return Dis_point_line(p, v); // 点的投影在线段上
}
int Line_relation(Line v1, Line v2) { // 两条直线的位置关系
    if (sgn(Cross(v1.p2 - v1.p1, v2.p2 - v2.p1)) == 0) {
        if (Point_line_relation(v1.p1, v2) == 0) return 1; // 重合
        else return 0; // 平行
    }
    return 2; // 相交
}
Point Cross_point(Point a, Point b, Point c, Point d) { // 两条直线的交点
    double s1 = Cross(b - a, c - a);
    double s2 = Cross(b - a, d - a);
    return Point(c.x * s2 - d.x * s1, c.y * s2 - d.y * s1) / (s2 - s1);
    // 调用前保证s2-s1 != 0，即直线AB和CD不共线也不平行
}
bool Cross_segment(Point a, Point b, Point c, Point d) {  // 判断两条线段是否相交
    double c1 = Cross(b - a, c - a), c2 = Cross(b - a, d - a);
    double d1 = Cross(d - c, a - c), d2 = Cross(d - c, b - c);
    return sgn(c1) * sgn(c2) < 0 && sgn(d1) * sgn(d2) < 0;
}
// 求两线段交点时，先判断线段是否相交，再利用两直线求交点

多边形

int Point_in_polygon(Point pt, Point* p, int n) { // 判断点pt和多边形的关系，*p为多边形
    for (int i = 0; i < n; i++) {
        if (p[i] == pt) return 3; // 点在多边形顶点上
    }
    for (int i = 0; i < n; i++) {
        Line v = Line(p[i], p[(i + 1) % n]);
        if (Point_on_seg(pt, v)) return 2; // 点在边上
    }
    int num = 0;
    for (int i = 0; i < n; i++) {
        int j = (i + 1) % n;
        int c = sgn(Cross(pt - p[j], p[i] - p[j]));
        int u = sgn(p[i].y - pt.y);
        int v = sgn(p[j].y - pt.y);
        if (c > 0 && u < 0 && v >= 0) num++;
        if (c < 0 && u >= 0 && v < 0) num--;
    }
    return num != 0; // 1：点在内部；0：点在外部
}
double Polygon_area(Point* p, int n) { // 多边形面积
    double area = 0;
    for (int i = 0; i < n; i++)
        area += Cross(p[i], p[(i + 1) % n]);
    return area / 2; // 面积有正负
}
Point Polygon_center(Point* p, int n) { // 求多边形重心
    Point ans(0, 0);
    if (Polygon_area(p, n)) return ans;
    for (int i = 0; i < n; i++)
        ans = ans + (p[i] + p[(i + 1) % n]) * Cross(p[i], p[(i + 1) % n]);
    return ans / Polygon_area(p, n) / 6;
}

凸包

判断多边形是否为凸包

#include <bits/stdc++.h>

using namespace std;
#define double long double

const int N = 2e5 + 5;
const double pi = acos(-1.0);
const double eps = 1e-8;

// 判断 x 的大小，<0 返回 -1，>0 返回 1，==0 返回 0
int sgn(double x) {
    if (fabs(x) < eps) return 0;
    else return x < 0 ? -1 : 1;
}

// 比较两个浮点数
int dcmp(double x, double y) {
    if (fabs(x - y) < eps) return 0;
    else return x < y ? -1 : 1;
}

struct Point {
    double x, y;
    Point() {}
    Point(double x, double y) : x(x), y(y) {}

    Point operator + (const Point& B) const { return Point(x + B.x, y + B.y); }
    Point operator - (const Point& B) const { return Point(x - B.x, y - B.y); }
    Point operator * (double k) const { return Point(x * k, y * k); }
    Point operator / (double k) const { return Point(x / k, y / k); }

    bool operator == (const Point& B) const {
        return sgn(x - B.x) == 0 && sgn(y - B.y) == 0;
    }
    bool operator < (const Point& B) const {
        return sgn(x - B.x) < 0 || sgn(x - B.x) == 0 && sgn(y - B.y) < 0;
    }
};

typedef Point Vector;

class Geometry {
public:
    static double Dot(const Vector& A, const Vector& B) {
        return A.x * B.x + A.y * B.y;
    }

    static int AngleJudge(const Vector& A, const Vector& B) {
        return sgn(Dot(A, B));
    }

    static double Len(const Vector& A) {
        return sqrt(Dot(A, A));
    }

    static double Angle(const Vector& A, const Vector& B) {
        return acos(Dot(A, B) / Len(A) / Len(B));
    }

    static double Cross(const Vector& A, const Vector& B) {
        return A.x * B.y - A.y * B.x;
    }
};
struct cmp {
    bool operator ()(Point x, Point y) const {
        if (x.x == y.x) {
            return x.y < y.y;
        } else return x.x < y.x;
    }
};

int n;
Point p[N];

bool isConvexPolygon() {
    if (n < 3) return false;

    set<Point, cmp> st;
    for (int i = 0; i < n; i++) {
        st.insert(p[i]);
    }
    if (st.size() < n) {
        return false;
    }

    bool f1 = 1, f2 = 1;
    double sum = 0;
    for (int i = 0; i < n; i++) {
        int x = (i - 1 + n) % n;
        int y = (i + 1 + n) % n;
        Vector t = p[x] - p[i];
        Vector g = p[y] - p[i];
        double tt = -atan2(g.y, g.x) + atan2(t.y, t.x);
        if (tt < 0) tt += 2 * pi;
        if (Geometry::Cross(g, t) <= 0) {
            f1 = 0;
            break;
        }
        sum += tt;
    }
    if (sgn(sum - (n - 2) * pi) != 0) f1 = 0;

    sum = 0;
    for (int i = 0; i < n; i++) {
        int x = (i - 1 + n) % n;
        int y = (i + 1 + n) % n;
        Vector t = p[x] - p[i];
        Vector g = p[y] - p[i];
        double tt = atan2(g.y, g.x) - atan2(t.y, t.x);
        if (tt < 0) tt += 2 * pi;
        if (Geometry::Cross(t, g) <= 0) {
            f2 = 0;
            break;
        }
        sum += tt;
    }
    if (sgn(sum - (n - 2) * pi) != 0) f2 = 0;

    if (f1 || f2) return true;
    return false;

}


int main() {
    std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);

    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> p[i].x >> p[i].y;
    }

    cout << (isConvexPolygon() ? "Yes\n" : "No\n");

}

方法 2：

求凸包周长

例: P2742 [USACO5.1] 圈奶牛Fencing the Cows /【模板】二维凸包

给定 n 个点的坐标, 求凸包周长.

double Distance(Point A, Point B) { return hypot(A.x - B.x, A.y - B.y); }
int Convex_hull(Point* p, int n, Point* ch) { // ch放凸包顶点，返回值是顶点个数
    n = unique(p, p + n) - p; // 去重
    sort(p, p + n);
    int v = 0;
    for (int i = 0; i < n; i++) {
        while (v > 1 && sgn(Cross(ch[v - 1] - ch[v - 2], p[i] - ch[v - 1])) <= 0)
            v--;
        ch[v++] = p[i];
    }
    int j = v;
    // 求上凸包
    for (int i = n - 2; i >= 0; i--) {
        while (v > j && sgn(Cross(ch[v - 1] - ch[v - 2], p[i] - ch[v - 1])) <= 0)
            v--;
        ch[v++] = p[i];
    }
    if (n > 1) v--;
    return v;
}
Point p[N], ch[N];
// int v = Convex_hull(p, n, ch);

凸包直径

https://www.luogu.com.cn/problem/P1452

class Geometry {
public:
    static double Cross(const Vector& A, const Vector& B) {
        return A.x * B.y - A.y * B.x;
    }
};

int n, m;
int sta[N], top;  // 将凸包上的节点编号存在栈里，第一个和最后一个节点编号相同
Point a[N], ch[N];
ll mx;

ll pf(ll x) { return x * x; }

ll dis(int p, int q) { return pf(ch[p].x - ch[q].x) + pf(ch[p].y - ch[q].y); }

ll sqr(int p, int q, int y) {
    return abs(Geometry::Cross((ch[q] - ch[p]), (ch[y] - ch[q])));
}

int Convex_hull(Point* p, int n, Point* ch) { // ch放凸包顶点，返回值是顶点个数
    n = unique(p, p + n) - p; // 去重
    sort(p, p + n);
    int v = 0;
    for (int i = 0; i < n; i++) {
        while (v > 1 && sgn(Geometry::Cross(ch[v - 1] - ch[v - 2], p[i] - ch[v - 1])) <= 0)
            v--;
        ch[v++] = p[i];
    }
    int j = v;
    // 求上凸包
    for (int i = n - 2; i >= 0; i--) {
        while (v > j && sgn(Geometry::Cross(ch[v - 1] - ch[v - 2], p[i] - ch[v - 1])) <= 0)
            v--;
        ch[v++] = p[i];
    }
    if (n > 1) v--;
    return v;
}

void get_longest() {  // 求凸包直径
    mx = 0;
    int j = 3;
    if (top < 3) {
        mx = dis(sta[1], sta[2]);
        return;
    }
    for (int i = 1; i <= top; ++i) {
        while (sqr(sta[i], sta[i + 1], sta[j]) <=
            sqr(sta[i], sta[i + 1], sta[j % top + 1]))
            j = j % top + 1;
        mx = max(mx, max(dis(sta[i + 1], sta[j]), dis(sta[i], sta[j])));
    }
}

int main() {
    top = 0;
    cin >> n;
    for (int i = 0; i < n; i++) cin >> a[i].x >> a[i].y;
    int v = Convex_hull(a, n, ch); // 先求凸包
    for (int i = 1; i <= v; i++) sta[++top] = i - 1; // sta存储点的下标
    sta[v + 1] = 0; // 封闭图形，多放的是第一个点的下标
    get_longest(); // 求凸包直径，该题输出直径的平方
    cout << mx << '\n';
}

平面最近点对

P1257 平面上的最接近点对

#include <bits/stdc++.h>
using namespace std;
const double eps = 1e-8;
const int N = 1e4 + 5;
const double INF = 1e20;
int sgn(double x) {
    if (fabs(x) < eps) return 0;
    return x < 0 ? -1 : 1;
}
struct Point {
    double x, y;
};
double Distance(Point A, Point B) {
    return hypot(A.x - B.x, A.y - B.y);
}
bool cmpxy(Point A, Point B) {
    return sgn(A.x - B.x) < 0 || (sgn(A.x - B.x) == 0 && sgn(A.y - B.y) < 0);
}
bool cmpy(Point A, Point B) { return sgn(A.y - B.y) < 0; }
Point p[N], tmp_p[N];
double Closest_Pair(int left, int right) {
    double dis = INF;
    if (left == right) return dis;
    if (left + 1 == right) return Distance(p[left], p[right]);
    int mid = (right + left) / 2;
    double d1 = Closest_Pair(left, mid);
    double d2 = Closest_Pair(mid + 1, right);
    dis = min(d1, d2);
    int k = 0;
    for (int i = left; i <= right; i++)
        if (fabs(p[mid].x - p[i].x) <= dis)
            tmp_p[k++] = p[i];
    sort(tmp_p, tmp_p + k, cmpy); // 按y排序，用于剪枝
    for (int i = 0; i < k; i++)
        for (int j = i + 1; j < k; j++) {
            if (tmp_p[j].y - tmp_p[i].y >= dis) break;
            dis = min(dis, Distance(tmp_p[i], tmp_p[j]));
        }
    return dis;
}
int main()
{
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%lf %lf", &p[i].x, &p[i].y);
    }
    sort(p, p + n, cmpxy);
    printf("%.4f\n", Closest_Pair(0, n - 1));
    return 0;
}

圆

struct Circle {
    Point c;
    double r;
    Circle() {}
    Circle(Point c, double r) :c(c), r(r) {}
    Circle(double x, double y, double _r) { c = Point(x, y), r = _r; }
};
int Point_circle_relation(Point p, Circle C) {
    double dst = Distance(p, C.c);
    if (sgn(dst - C.r) < 0) return 0; // 点在圆内
    if (sgn(dst - C.r) == 0) return 1; // 点在圆上
    return 2; // 点在圆外
}
int Line_circle_relation(Line v, Circle C) {
    double dst = Dis_point_line(C.c, v);
    if (sgn(dst - C.r) < 0) return 0; // 直线和圆相交
    if (sgn(dst - C.r) == 0) return 1; // 直线和圆相切
    return 2; // 直线和圆相离
}
int Seg_circle_relation(Segment v, Circle C) {
    double dst = Dis_point_line(C.c, v);
    if (sgn(dst - C.r) < 0) return 0; // 线段和圆相交
    if (sgn(dst - C.r) == 0) return 1; // 线段和圆相切
    return 2; // 线段和圆相离
}
int Line_cross_circle(Line v, Circle C, Point& pa, Point& pb) {
    // 返回值是交点个数，pa和pb是交点
    if (Line_circle_relation(v, C) == 2) return 0; // 无交点
    Point q = Point_line_proj(C.c, v); // 圆心在直线上的投影点
    double d = Dis_point_line(C.c, v);
    double k = sqrt(C.r * C.r - d * d);
    if (sgn(k) == 0) {
        pa = q; pb = q; return 1; // 直线和圆相切
    }
    Point n = (v.p2 - v.p1) / Len(v.p2 - v.p1); // 单位向量
    pa = q + n * k; pb = q - n * k;
    return 2; // 两个交点
}

最小圆覆盖

P1742 最小圆覆盖

三维几何板子

点&向量

struct Point3 {
    double x, y, z;
    Point3() {}
    Point3(double x, double y, double z) :x(x), y(y), z(z) {}
    Point3 operator + (Point3 B) { return Point3(x + B.x, y + B.y, z + B.z); }
    Point3 operator - (Point3 B) { return Point3(x - B.x, y - B.y, z - B.z); }
    Point3 operator * (double k) { return Point3(x * k, y * k, z * k); }
    Point3 operator / (double k) { return Point3(x / k, y / k, z / k); }
    bool operator == (Point3 B) {
        return sgn(x - B.x) == 0 &&
            sgn(y - B.y) == 0 && sgn(z - B.z) == 0;
    }
};
typedef Point3 Vector3; // 三维向量
double Distance(Vector3 A, Vector3 B) {
    return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y) + (A.z - B.z) * (A.z - B.z));
}

直线&线段

struct Line3 {
    Point3 p1, p2;
    Line3() {}
    Line3(Point3 p1, Point3 p2) :p1(p1), p2(p2) {}
};
typedef Line3 Segment3;
double Dot(Vector3 A, Vector3 B) { return A.x * B.x + A.y * B.y + A.z * B.z; }
double Len(Vector3 A) { return sqrt(Dot(A, A)); }
double Len2(Vector3 A) { return Dot(A, A); }
double Angle(Vector3 A, Vector3 B) { return acos(Dot(A, B) / Len(A) / Len(B)); }
Vector3 Cross(Vector3 A, Vector3 B) {
    return Point3(A.y * B.z - A.z * B.y, A.z * B.x - A.x * B.z, A.x * B.y - A.y * B.x);
}
double Area2(Point3 A, Point3 B, Point3 C) { return Len(Cross(B - A, C - A)); }
bool Point_trangle_relation(Point p, Point A, Point B, Point C) {
    // 返回1表示点p在三角形内
    return dcmp(Area2(p, A, B) + Area2(p, B, C) + Area2(p, C, A), Area2(A, B, C)) == 0;
}
bool Point_line_relation(Point3 p, Line3 v) { // 1表示点在直线上
    return sgn(Len(Cross(v.p1 - p, v.p2 - p))) == 0 && sgn(Dot(v.p1 - p, v.p2 - p)) == 0;
}
double Dis_point_seg(Point3 p, Segment3 v) {
    if (sgn(Dot(p - v.p1, v.p2 - v.p1)) < 0 || sgn(Dot(p - v.p2, v.p1 - v.p2)) < 0)
        return min(Distance(p, v.p1), Distance(p, v.p2));
}
Point3 Point_line_proj(Point3 p, Line3 v) {
    double k = Dot(v.p2 - v.p1, p - v.p1) / Len2(v.p2 - v.p1);
    return v.p1 + (v.p2 - v.p1) * k;
}

平面

struct Plane { // 三维平面
    Point3 p1, p2, p3;
    Plane() {}
    Plane(Point3 p1, Point3 p2, Point3 p3) :p1(p1), p2(p2), p3(p3) {}
};
Point3 Pvec(Point3 A, Point3 B, Point3 C) { return Cross(B - A, C - A); } // 平面法向量
Point3 Pvec(Plane f) { return Cross(f.p2 - f.p1, f.p3 - f.p1); }
bool Point_on_plane(Point3 A, Point3 B, Point3 C, Point3 D) { // 四点共平面
    return sgn(Dot(Pvec(A, B, C), D - A)) == 0;
}
// 两平面平行
int Parallel(Plane f1, Plane f2) { return Len(Cross(Pvec(f1), Pvec(f2))) < eps; }
// 两平面垂直
int Vertical(Plane f1, Plane f2) { return sgn(Dot(Pvec(f1), Pvec(f2))) == 0; }
int Line_cross_plane(Line3 u, Plane f, Point3& p) { // 直线和平面的交点
    Point3 v = Pvec(f);
    double x = Dot(v, u.p2 - f.p1);
    double y = Dot(v, u.p1 - f.p1);
    double d = x - y;
    if (sgn(x) == 0 && sgn(y) == 0) return -1; // v在f上
    if (sgn(d) == 0) return 0; // v与f平行
    p = ((u.p1 * x) - (u.p2 * y)) / d; // v与f相交
    return 1;
}

其他

double volume4(Point3 a, Point3 b, Point3 c, Point3 d) { // 四面体有向体积*6
    return Dot(Cross(b - a, c - a), d - a);
}

极角排序

我们知道，一个点的坐标可以转化为极坐标，其中极角的范围是 \([0, 2\pi)\) ，那么可以根据这个角度对所有点进行排序。

（long）double 排序

这种方式常数小，但会损失精度。

atan2(y,x)，表示 \((x, y)\) 这个点与原点连线，这条线与x轴正半轴的夹角，这里的这个极角的范围是 \([−\pi,\pi]\) 的，一二象限为正，三四象限为负。

从小到大排完序后，实际上是第三象限→第四象限→第一象限→第二象限。

struct Point{
    int x, y;
    double angle;
    bool operator < (const node &t) const{
        return angle < t.angle;
    }
};
for (int i = 1; i <= n; i++){
    cin >> p[i].x >> p[i].y;
    p[i].angle = atan2(p[i].y, p[i].x);
}
sort(p + 1, p + n + 1, cmp);

// 或
using Points = vector<Point>;
double theta(auto p) { return atan2(p.y, p.x); } // 求极角
void psort(Points &ps, Point c = O)              // 极角排序
{
    sort(ps.begin(), ps.end(), [&](auto p1, auto p2) {
        return lt(theta(p1 - c), theta(p2 - c));
    });
}

long long 叉积排序

这种方式常数大，但若所有的点坐标都是整数，会避免所有的精度问题。

以下代码排序后，得到的顺序是从 x 正半轴开始逆时针旋转扫过的位置。

struct Point {
    ll x, y;
    ll operator * (const Point& p) const {
        return x * p.y - y * p.x;
    }
};
int f(Point a) {
    if (a.x > 0 && a.y >= 0) return 1; // 第一象限和x正半轴
    if (a.x <= 0 && a.y > 0) return 2; // 第二象限和y正半轴
    if (a.x < 0 && a.y <= 0) return 3; // 第三象限和x负半轴
    if (a.x >= 0 && a.y < 0) return 4; // 第四象限和y负半轴
    return 0;
}
bool cmp(Point a, Point b) {
    if (f(a) != f(b)) return f(a) < f(b);
    return a * b > 0;
}

Point points[N];
sort(points, points + n, cmp);

例题1-2021 ICPC 澳门 C

题意：给定 n 个整数坐标点，任意两点都有一条连线，求至少要删除多少个点，才能让原点不被剩余点的连线包围住？题目保证没有连线会经过原点。

分析：若要满足题意，则剩余的点必定在以原点为顶点的180°范围之内。对给出的点进行极角排序，双指针枚举进行遍历，更新答案。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e6 + 5;
struct Point {
    ll x, y;
    ll operator * (const Point& p) const {
        return x * p.y - y * p.x;
    }
}points[N * 2];
int f(Point a) {
    if (a.x > 0 && a.y >= 0) return 1;
    if (a.x <= 0 && a.y > 0) return 2;
    if (a.x < 0 && a.y <= 0) return 3;
    if (a.x >= 0 && a.y < 0) return 4;
    return 0;
}
bool cmp(Point a, Point b) {
    if (f(a) != f(b)) return f(a) < f(b);
    return a * b > 0;
}
int n;
void solve()
{
    cin >> n;
    for (int i = 0; i < n; i++) {
        int x, y;
        cin >> x >> y;
        points[i] = {x, y};
    }
    sort(points, points + n, cmp);
    for (int i = 0; i < n; i++) points[i + n] = points[i];
    int l = 0, r = 0;
    int ans = 0;
    while (l < n) {
        r = max(r, l);
        Point c;
        // c是p[l]关于原点的对称点
        c.x = -points[l].x, c.y = -points[l].y;
        // p[r]在p[l]和c构成的半圆范围内
        while (r - l < n && points[r] * c >= 0) {
            r++;
        }
        ans = max(ans, r - l);
        l++;
    }
    cout << n - ans << '\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T;
    cin >> T;
    while (T--)
        solve();
}

距离

欧式距离

\[ 二维：|AB|=\sqrt[]{(x_1-x_2)^2 + (y_1-y_2)^2} \]

\[ 三维：|AB|=\sqrt[]{(x_1-x_2)^2 + (y_1-y_2)^2 + (z_1-z_2)^2} \]

曼哈顿距离

定义

在二维空间内，两个点之间的曼哈顿距离（Manhattan distance）为它们横坐标之差的绝对值与纵坐标之差的绝对值之和。则 A \((x_1, y_1)\)，B \((x_2, y_2)\) 之间的曼哈顿距离用公式可以表示为： $$ d(A,B)=|x_1-x_2|+|y_1-y_2| $$

性质

• 非负性：曼哈顿距离是一个非负数
• 统一性：点到自身的曼哈顿距离为 0
• 对称性：A 到 B的距离与 B 到 A 的距离相等
• 三角不等式：从点 i 到点 j 的直接距离不会大于途径任何其他点 k 的距离

切比雪夫距离

定义

切比雪夫距离（Chebyshev distance）是向量空间中的一种度量，二个点之间的距离定义为其各坐标数值差的最大值。 $$ d(A,B)=max(|x_1-x_2|,|y_1-y_2|) $$ 可以理解为从一个点出发，可以往上下左右 左上 左下 右上 右下 8个方向前进，到达另一个点所需的最小步数。

切比雪夫距离与曼哈顿距离的相互转化

曼哈顿坐标系是通过切比雪夫坐标系旋转45°后，再缩小到原来的一半得到的。

将一个点 \((x, y)\) 的坐标变为 \((x+y, x-y)\) 后，原坐标系中的曼哈顿距离等于新坐标系中的切比雪夫距离。

将一个点 \((x, y)\) 的坐标变为 \((\frac{(x+y)}{2}, \frac{(x-y)}{2})\) 后，原坐标系中的切比雪夫距离等于新坐标系中的曼哈顿距离。

给定两矩形求重叠面积

while(scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&a,&b,&c,&d,&e,&f,&g,&h)!=EOF) {
    s = 0.00;
    double x1,y1,x2,y2,x3,y3,x4,y4;

    x1 = min(a,c); x2 = max(a,c);       //确保对角线的点是左下和右上
    x3 = min(e,g); x4 = max(e,g);
    y1 = min(b,d); y2 = max(b,d);
    y3 = min(f,h); y4 = max(f,h);

    double left = max(x1,x3);
    double right = min(x2,x4);
    double up = min(y2,y4);
    double down = max(y1,y3);
    //printf("%f %f %f %f\n",left,right,up,down);
    if(left < right && up > down) s = (right-left)*(up-down);
    printf("%.2lf\n",s);
}

半平面交

# P4196 [CQOI2006] 凸多边形 /【模板】半平面交

逆时针给出 \(n\) 个凸多边形的顶点坐标，求它们交的面积。例如 \(n=2\) 时，两个凸多边形如下图：

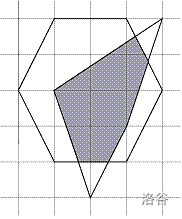
则相交部分的面积为 \(5.233\)。

解法

https://zhuanlan.zhihu.com/p/666868712

代码

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 5e2 + 5;

const double pi = acos(-1.0);
const double eps = 1e-8;

// 判断 x 的大小，<0 返回 -1，>0 返回 1，==0 返回 0
int sgn(double x) {
    if (fabs(x) < eps) return 0;
    else return x < 0 ? -1 : 1;
}

// 比较两个浮点数
int dcmp(double x, double y) {
    if (fabs(x - y) < eps) return 0;
    else return x < y ? -1 : 1;
}

struct Point {
    double x, y;
    double angle;
    Point() {}
    Point(double x, double y) : x(x), y(y) {}

    Point operator + (const Point& B) const { return Point(x + B.x, y + B.y); }
    Point operator - (const Point& B) const { return Point(x - B.x, y - B.y); }
    Point operator * (double k) const { return Point(x * k, y * k); }
    Point operator / (double k) const { return Point(x / k, y / k); }

    bool operator == (const Point& B) const {
        return sgn(x - B.x) == 0 && sgn(y - B.y) == 0;
    }
    // bool operator < (const Point& B) const {
    //     return sgn(x - B.x) < 0 || sgn(x - B.x) == 0 && sgb(y - B.y) < 0;
    // }
    bool operator < (const Point& B) const {
        return angle < B.angle;
    }
};

typedef Point Vector;

class Geometry {
public:
    static double Cross(const Vector& A, const Vector& B) {
        return A.x * B.y - A.y * B.x;
    }

    static double Area2(const Point& A, const Point& B, const Point& C) {
        return Cross(B - A, C - A);
    }
};

class Line {
public:
    Point p1, p2;

    Line() {}
    Line(Point p1, Point p2) : p1(p1), p2(p2) {}
    Line(Point p, double angle) {
        p1 = p;
        if (sgn(angle - pi / 2) == 0) {
            p2 = p1 + Point(0, 1);
        } else {
            p2 = p1 + Point(1, tan(angle));
        }
    }
    Line(double a, double b, double c) {
        if (sgn(a) == 0) {
            p1 = Point(0, -c / b);
            p2 = Point(1, -c / b);
        } else if (sgn(b) == 0) {
            p1 = Point(-c / a, 0);
            p2 = Point(-c / a, 1);
        } else {
            p1 = Point(0, -c / b);
            p2 = Point(1, (-c - a) / b);
        }
    }

    int PointLineRelation(const Point& p) const {
        int c = sgn(Geometry::Cross(p2 - p1, p - p1));
        if (c < 0) return 1; // p 在 v 的右侧
        if (c > 0) return 2; // p 在 v 的左侧
        return 0; // p 在 v 上
    }

    static Point CrossPoint(const Point& a, const Point& b, const Point& c, const Point& d) {
        double s1 = Geometry::Cross(b - a, c - a);
        double s2 = Geometry::Cross(b - a, d - a);
        return Point(c.x * s2 - d.x * s1, c.y * s2 - d.y * s1) / (s2 - s1);
    }

    static Point CrossPoint(const Line& a, const Line& b) {
        return Line::getLineIntersection(a.p1, a.p2 - a.p1, b.p1, b.p2 - b.p1);
    }

    static Point getLineIntersection(const Point& p, const Point& v, const Point& q, const Point& w) {
        Point u = p - q;
        double t = Geometry::Cross(w, u) / Geometry::Cross(v, w);
        return {p.x + v.x * t, p.y + v.y * t};
    }

    static double getAngle(const Line& a) {
        return atan2(a.p2.y - a.p1.y, a.p2.x - a.p1.x);
    }

    // b和c的交点是否在a的右侧
    static bool onRight(const Line& a, const Line& b, const Line& c) {
        return a.PointLineRelation(Line::CrossPoint(b, c)) <= 1;
    }
};

int n;
int cnt;
int q[N];
Point pg[N];
Point res[N];
Line line[N];

void solve() {
    cin >> n;
    for (int i = 0; i < n; i++) {
        int m;
        cin >> m;
        for (int j = 0; j < m; j++) {
            cin >> pg[j].x >> pg[j].y;
        }
        for (int j = 0; j < m; j++) {
            line[cnt++] = {pg[j], pg[(j + 1) % m]};
        }
    }

    // 极角排序
    sort(line, line + cnt, [&](const Line& a, const Line& b) {
        double A = Line::getAngle(a), B = Line::getAngle(b);
        if (!dcmp(A, B)) return Geometry::Area2(a.p1, a.p2, b.p2) < 0;
        return A < B;
        });

    int hh = 0, tt = -1;
    for (int i = 0; i < cnt; i++) {
        // 角度相同的直线只考虑最靠左的一条,显然只有靠近左边的是有效的
        if (i && !dcmp(Line::getAngle(line[i]), Line::getAngle(line[i - 1]))) continue;
        // 删除队尾没有贡献的线段
        while (hh + 1 <= tt && Line::onRight(line[i], line[q[tt - 1]], line[q[tt]])) tt--;
        // 删除队头没有贡献的线段
        while (hh + 1 <= tt && Line::onRight(line[i], line[q[hh]], line[q[hh + 1]])) hh++;
        // 如果可以构成轮廓，将当前直线加入队列
        q[++tt] = i;
    }

    // 队头、队尾相互更新，还要确保队尾和队头都是有效的
    while (hh + 1 <= tt && Line::onRight(line[q[hh]], line[q[tt - 1]], line[q[tt]])) tt--;
    while (hh + 1 <= tt && Line::onRight(line[q[tt]], line[q[hh]], line[q[hh + 1]])) hh++;
    // 让轮廓闭合
    q[++tt] = q[hh];
    // 轮廓求出来后，求出轮廓的所有顶点
    int k = 0;
    for (int i = hh; i < tt; i++) res[k++] = Line::CrossPoint(line[q[i]], line[q[i + 1]]);
    // 求凸包面积
    double ans = 0;
    for (int i = 1; i + 1 < k; i++) ans += Geometry::Area2(res[0], res[i], res[i + 1]);
    cout << fixed << setprecision(3) << ans / 2 << '\n';
}

int main() {
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int _T = 1;
    // cin >> _T;
    while (_T--)
        solve();
    return 0;
}